Sammenstilling av data

I denne artikkelen vil vi nøste sammen noen tråder om statistikk.
Hvor mange er nok?
Statistikk handler om å bruke utvalg til å trekke slutninger om en større populasjon (1-4). Hvis et utvalg skal gi sikker kunnskap om populasjonen må vi sørge for at utvalget er representativt og at utvalget består av tilstrekkelig mange deltakere. Tilstrekkelig mange er ikke et tall, og i forkant av kliniske studier må forskerne gjøre en jobb for å finne ut hvor mange deltakere som må inkluderes for at deres studie skal inkludere tilstrekkelig mange. Planleggingen kalles gjerne statistisk forsøksplanlegging og innebærer at forskerne må veie fordeler og ulemper med å inkludere mange deltakere opp mot hverandre. Inkluderer de for få pasienter risikerer de at studien gir upresise data og usikre konklusjoner. For mange deltakere vil på en annen side koste unødvendig mye tid og ressurser.
Uavhengige forskningsmiljøer
Tenk deg nå en forsker som ønsker å teste effekten av en ny medisin. Gjennom forsøksplanlegging har forskeren fått vite at de må inkludere 1000 deltakere for å kunne vente et fullgodt svar på om medisinen virker. Det vil ta forskeren mange år å rekruttere så mange som 1000 deltakere, og i realismens navn begrenser forskeren ambisjonsnivået til inklusjon av 200 pasienter. Den ene halvparten får medisin, og den andre halvparten får narremedisin (placebo). Når studien avsluttes finner forskeren at gjennomsnittlig smerteskår var 0,29 poeng lavere blant dem som fikk aktiv behandling enn i placebogruppen. Konfidensintervallet strekker seg fra -0,08 til 0,67 så forskjellen er ikke statistisk signifikant (P=0,124) (2). Forskjellen på 0,29 poeng er med andre ord ikke større enn at den kan skyldes tilfeldighetenes spill, men det betyr ikke at vi kan utelukke at det er en forskjell mellom de to gruppene. Hvis forskeren hadde inkludert flere deltakere i studien sin ville konfidensintervallet blitt smalere og forskjellen tydeligere.
Heldigvis viser det seg at flere uavhengige forskningsmiljøer har hatt interesse av å finne svar på det samme spørsmålet. Samtidig som vår forsker gjennomførte sin studie av 200 pasienter, har fire uavhengige forskningsmiljøer gjort det samme. Alle miljøene har inkludert 200 pasienter, kriteriene for inklusjon av pasienter er de samme og behandlingsoppleggene er identiske. Totalt har vi altså tilgang til fem studier av i alt 1000 pasienter (figur 1). Hver studie gir effektestimat og konfidensintervall for forskjellen mellom behandling og kontroll. Siden hver enkeltstudie baserer seg på en ny stikkprøve (utvalg) kan vi ikke vente at de fem studiene ender opp med identiske resultater.
Når kan vi slå sammen studier?
Så lenge deltakerne er behandlet på samme måte i alle tilgjengelige studier kan vi være ganske sikre på at variasjonen vi ser mellom studier skyldes tilfeldig variasjon. Da kan det være fristende å slå sammen dataene fra de fem analysene siden vi da får mange flere observasjoner å basere oss på. Hvis vi slår sammen de fem studiene i det som kalles en metaanalyse (analyse av analyse) finner vi at gjennomsnittspasienten opplever større bedring (0,55 poeng) med medisin sammenliknet med narremedisin (figur 1). Konfidensintervallet strekker seg fra 0,37 til 0,73. Konfidensintervallet for totalen er smalere enn for enkeltstudiene hver for seg fordi mer data gir mindre usikkerhet, akkurat på samme måte som enkeltstudier med mange deltakere gir mer presise resultater enn enkeltstudier med få deltakere (1). Figuren vi bruker til å visualisere sammenstillingen av flere studier kalles forestplot (figur 1). I et forestplott framkommer totalen vanligvis som en diamantlignende form der bredden på diamanten tilsvarer konfidensintervallet til totalen.
Metaanalyser handler om å slå sammen resultater av studier som er forskjellige, men som har så store fellestrekk at man venter sammenliknbare resultater. Hvis du synes den formuleringen er ullen, så er det ikke annet å si enn at du har helt rett. En av de største utfordringene man står overfor når man planlegger metaanalyser er å definere hva som er likt nok til å slås sammen. Svaret på dette spørsmålet vil alltid avhenge av skjønnsmessige vurderinger, og det finnes ingen konsensusgaranti.
Hvordan slå sammen studier?
Generelt kan vi si at studier må rapportere resultater på samme skala for å tillate sammenslåing, men akkurat som i enkeltstudier kan du velge mellom ulike effektmål (3). Dikotome utfallsmål presenteres gjerne i form av risiko- eller oddsforhold (3). For forskjeller som er målt på kontinuerlig skala er ofte gjennomsnittsforskjeller (MD) å foretrekke, men fra tid til annen kan du komme over metaanalyser som beregner standardiserte gjennomsnittsforskjeller (SMD). SMD brukes når man ønsker å slå sammen studier som har målt tilnærmet samme utfall på ulike skalaer, for eksempel to ulike livskvalitetsskalaer, men SMD har den ulempen at tallene er vanskelig å fortolke i praksis.
En helt essensiell del av en metaanalyse er å avgjøre om noen studier bør tillegges større vekt enn andre, for eksempel virker det ganske logisk å legge større vekt på store studier enn på små. Hvor stor vekt som skal legges på hver studie bestemmes gjerne automatisk (matematisk), men de som lager metaanalysene må velge hvilke statistiske og matematiske modeller som skal bestemme hvilken vekt hver enkeltstudie skal få (5). Om man velger tilfeldig (random) eller fiksert (fixed) effektmodell (5) vil også ha betydning for vektingen av studier.
Når du leser metaanalyser kan du vanligvis se hvilken vekt som er tillagt hver studie på to måter. Ofte er vekting eksplisitt beskrevet, andre ganger kan vektingen leses indirekte ut av forestplottet (figur 2).

Tveeggete sverd
Studier vi sammenstiller i metaanalyser er aldri helt identiske. Det har både positive og negative sider. Det at studiene er gjennomført i forskjellige kontekster, på ulike pasienter og av ulikt personell, betyr på den ene siden at metaanalyser ofte kan generaliseres til en bredere setting enn enkeltstudiene hver for seg. Tenk for eksempel at vi har tilgang til fem enkeltstudier som inkluderer pasienter med ulik sykdomsalvorlighet og ulik grad av komorbiditet. Metaanalyse av de samme fem studiene sier da noe om hvilke resultater vi kan forvente på tvers av sykdomsalvorlighet og grad av komorbiditet.
Uheldigvis er metaanalysens styrke også en akilleshæl. Blir man for ivrig risikerer man å slå sammen studier som er så forskjellige at det er meningsløst å generalisere på tvers. Dette poenget framkommer ganske tydelig fra forestplottene i figur 3. I figur 3A viser de inkluderte enkeltstudiene konsistente resultater, og det virker rimelig å generalisere på tvers. I figur 3B avviker én av enkeltstudiene fra de andre, men vi kan fortsatt argumentere for at det er fornuftig å sammenlikne resultater på tvers. Figur 3C illustrerer en metaanalyse der tre studier viser positiv effekt av behandling mens to studier viser negativ effekt. Totalen viser at behandlingen ikke har effekt, men kan vi tro på det? Hvis de tre studiene som viser positiv effekt er gjort på eldre pasienter mens de to studiene som viser negativ effekt er gjort blant folk under 30, blir det ganske meningsløst å generalisere på tvers og konkludere at behandlingen ikke har effekt.
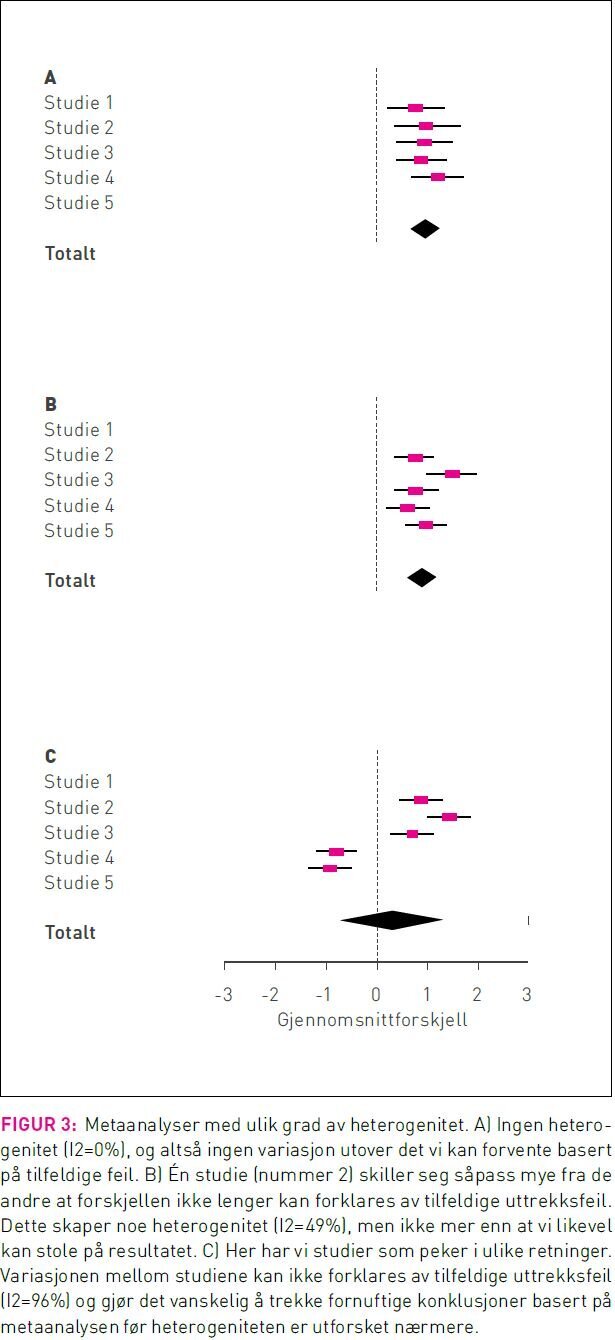
Inkonsistens
I metaanalyser omtales variasjon på tvers av studier som inkonsistens eller heterogenitet. Visuell inspeksjon av forestplott er den enkleste og kanskje også den beste måten vi kan vurdere inkonsistens. Da får man raskt et inntrykk av om resultatene varierer mye på tvers av ulike studier og om konfidensintervallene overlapper. I tillegg til denne visuelle vurderingen er det mulig å gjennomføre statistiske tester og beregninger som beskriver graden av inkonsistens.
Den statistiske testen for heterogenitet tester hvor sannsynlig det er at alle tilgjengelige studier har samme underliggende effekt, lav p-verdi på denne testen tyder på inkonsistens (6). Grad av inkonsistens/heterogenitet oppgis også ofte i form av et måltall som kalles I2 (6). I2 tar verdier mellom 0 og 100 prosent og viser hvor mye av den totale variasjonen som ikke kan forklares av tilfeldige feil. Høy I2 tyder på at det er reelle forskjeller mellom studiene som er inkludert i metaanalysen – en advarsel om at det å slå sammen de aktuelle enkeltstudiene muligens ikke gir et meningsfylt resultat.
Noen ganger kan det være aktuelt å utforske heterogenitet ved å gruppere de ulike analysene etter andre faktorer som for eksempel alder eller geografisk lokalisering (subgrupper). Dette kalles gjerne subgruppeanalyser. Som alltid må man være forsiktig med slike retrospektive analyser. Det at en studie i retrospekt viser seg ikke å passe inn er et dårlig argument for å ta den bort. Interessante subgruppeanalyser skal helst være definert før vi ser resultatene av en metaanalyse, og inndelingen i subgrupper skal helst være basert på en plausibel årsaksmekanisme.
Referanser
- Brurberg KG, Hammer HL. Hvordan sammenlikne statistisk? Sykepleien Forskning. 2013;8:174 –7.
- Brurberg KG, Hammer HL. Hypotesetesting. Sykepleien Forskning. 2013;8:267–9.
- Brurberg KG, Hammer HL. Variabeltyper og dikotome effektmål. Sykepleien Forskning 2013; 8: 372–4.
- Hammer HL, Brurberg KG. Viktige modeller og begreper i statistikk. Sykepleien Forskning 2014; 9:84–8
- Smedslund G. Metaanalyser. Nor J Epidemiol 2013; 23: 147–149.
- Guyatt GH, Oxman AD, Kunz R et al. GRADE guidelines: 7. Rating the quality of evidence – inconsistency. Journal of clinical epidemiology 2011; 64:1294–302


















0 Kommentarer