Hvordan sammenlikne statistisk?

Vi har tidligere argumenterte for at grunnleggende forståelse av statistikk er viktig for å forstå forskningsartikler, og vi definerte sentrale begrep som statistiske fordelinger, populasjon og tilfeldige utvalg (1). I denne artikkelen skal strikken tøyes enda litt lenger, og vi skal se nærmere på hvordan vi kan bruke statistikk til å sammenlikne to grupper. Et eksempel kan være å sammenlikne en gruppe personer som har fått en bestemt type medisin med personer som bare har fått placebomedisin. Vårt mål er å gi leseren tilstrekkelig kunnskap til å forstå statistikken som svært mange forskningsartikler baserer seg på.

Gjennomsnitt og standardavvik

Det er kjent at høyt kolesterolnivå øker risikoen for hjerteinfarkt og andre karsykdommer. Vi ønsker nå å undersøke hvordan det står til med kolesterolnivået til nordmenn. Vi måler derfor kolesterolnivået til 30 tilfeldige nordmenn (tabell 1).

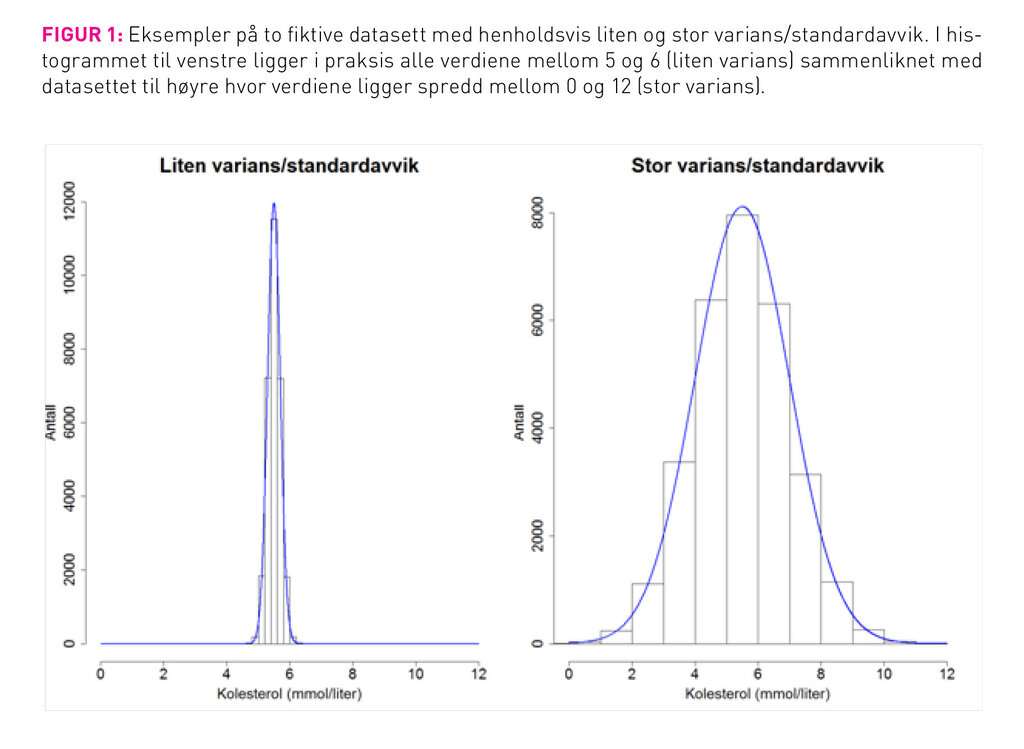
I mange forskningsartikler oppsummerer man et slikt datasett med to verdier, en for sentraltendens, for eksempel gjennomsnitt og en for variansen, for eksempel standardavvik. Gjennomsnittsverdier er kjent stoff for de fleste, og vi nøyer oss med å fortelle at gjennomsnittet for dette datasettet er 5,28 mmol/liter. Av det samme datasettet ser vi at verdiene varierer omtrentlig mellom 3,5 og 7,5 mmol/liter, og vi kan regne ut at standardavviket er 1,15. Hvordan kan du finne svar på andre steder (2), for de detaljene ønsker vi ikke å grave oss ned i her. Det som er viktig å vite er at standardavvik er tall som forteller oss hvor mye kolesterolet varierer mellom de ulike personene. I figur 1 viser vi to fiktive datasett, et med liten varians og et med stor varians.

Hva er konfidensintervall?

Tabell 1 viser hvordan det står til med kolesterolnivået til 30 enkeltpersoner, men vi er mer interessert i hvordan det står til med kolesterolnivået til hele den norske befolkningen (populasjonen). Siden de 30 personene er en del av befolkningen er det naturlig at de også kan fortelle en del om hvordan det står til i befolkningen. I de fleste situasjoner er det umulig å gjøre målinger for alle i hele landet (1), og derfor er vi nødt til å basere analysene på et tilfeldig utvalg som for eksempel de 30 personene. Vi trenger derfor et verktøy som systematisk kan benytte dataene fra et utvalg til å si noe konkret om hele befolkningen. Et konfidensintervall er nettopp et slikt verktøy. Her vil vi prøve å forklare hva resultatet betyr. Regner vi ut et 95 prosent konfidensintervall for dataene i tabell 1 vil vi få følgende resultat: [4.85, 5.71]. Det betyr at vi med 95 prosent sikkerhet kan si at det gjennomsnittlige kolesterolnivået til hele den norske befolkningen ligger et eller annet sted mellom 4,85 og 5,71 mmol/liter. Konfidensintervallet benytter altså de 30 tilgjengelige målingene til å si noe om hva slags resultat vi ville fått hvis vi hadde tatt oss bryet med å måle kolesterolet til alle i hele befolkningen og deretter beregnet gjennomsnittet. Det er kanskje ikke overraskende at konfidensintervall har stor nytteverdi innen forskning og andre steder hvor data analyseres.

Hva påvirker bredden?

Nå kunne vi kanskje tenkt oss et konfidensintervall som var smalere enn det vi fikk i avsnittet over. Det er i hovedsak to faktorer som gjør at et konfidensintervall blir bredt, stor varians i dataene og få målinger. Det finnes en måte å redusere variansen i en statistisk analyse, men det går utenfor hva vi kan skrive om her. Flere målinger vil også gjøre konfidensintervallet smalere fordi flere målinger rett og slett betyr at vi har mer informasjon om hele befolkningen og dermed kan vi med større sikkerhet si hva det gjennomsnittlige kolesterolnivået i befolkningen er. Hadde vi for eksempel hatt 3000 målinger i stedet for 30 målinger, men med samme gjennomsnitt og varians, ville konfidensintervallet blitt: [5.24, 5.32], altså mye smalere.

Så langt har vi kun sett på populasjonen som hele den norske befolkningen, men i praksis kan en populasjon vise til mye forskjellig. Ønsker vi å studere hvordan ulike kommuner har tilpasset seg en ny helsereform, vil populasjonen være alle norske kommuner og utvalget et tilfeldig utvalg av disse. Ønsker vi å studere kvaliteten på maten på et sykehus kan alle måltider som serveres på sykehuset gjennom året sees som en populasjon, mens utvalget er et sett tilfeldig valgte måltider. Ønsker vi å studere hvordan pasienter med forhøyet kolesterolnivå responderer på statiner kan populasjonen være alle nordmenn med totalkolesterol over en gitt grense. Men vi kan også peke ut en smalere populasjon ved å si at vi bare er interessert i dem som samtidig tilfredsstiller ett eller flere tilleggskriterier. Her kan det nevnes at variasjonen i et datasett kan påvirkes av hvordan populasjonen er definert. En snevert definert populasjon resulterer ofte i mindre naturlig variasjon og smalere konfidensintervall.

Hvordan måle forskjeller?

Vi har nå sett hvordan vi bruker statistikk til å si noe om en populasjon basert på et mindre utvalg. I enkelte sammenhenger, som for eksempel spørreundersøkelser og prevalensstudier, er det nettopp dette vi ønsker å bruke statistikken til. Andre ganger er vi mer interessert i å sammenlikne to grupper. Vi kan lure på om det er trening eller kognitiv behandling som hjelper best mot depresjon, eller om Birkendeltakelse øker risiko for hjerteinfarkt. I prinsippet åpner statistikken for å sammenlikne det meste, men det er en stor fordel hvis vi kan forutsette at de to gruppene vi sammenlikner er like ved oppstart. Tenk deg at vi sammenlikner risiko for hjerteinfarkt blant Birkendeltakere og en gruppe mennesker som mosjonerer jevnlig uten å delta i Birken, og vi ser at forekomsten av hjerteinfarkt er større blant Birkendeltakerne. Det er lett å hoppe raskt til en konklusjon, men vent! Er dette en rettferdig sammenlikning, eller kan forskjellen like gjerne skyldes at de som deltar i Birken har større konkurranseinstinkt, mer stressende jobber og generelt er mer stressete mennesketyper? Det finnes statistisk verktøy som kan justere for antatte ulikheter mellom grupper, men analysene blir mer komplekse og resultatene mer usikre enn når vi sammenlikner likt mot likt.

Den eneste måten vi kan være ganske sikre på at vi starter ut med å sammenlikne likt mot likt er ved randomisering hvor deltaker til de ulike gruppene er trukket ut tilfeldig. Et eksempel på dette ser vi i en norsk studie der forfatterne blant annet ønsker å undersøke om statiner (fluvastatin) har større innvirkning på kolesterolet enn placebomedisin (3). Forfatterne ønsker å kontrollere effekten blant stillesittende og overvektige menn som får medisiner mot høyt blodtrykk (populasjonen), og de rekrutterer 83 personer som blir tilfeldig fordelt til å få placebo-medisin (n=41) eller fluvastatin (n=42). Vi kan si at forfatterne har delt sitt opprinnelige utvalg inn i to mindre utvalg som hver for seg speiler den samme populasjonen.

Gjennomsnitt før og etter

Deler av resultatene fra fluvastatinstudien er oppsummert i tabell 2. Vi ser at gjennomsnittlig totalkolesterol ved oppstart er ganske likt (6,02 versus 5,88 mmol/liter). Den lille forskjellen kan enkelt forklares av tilfeldige feil (1). Mer interessant er det å studere medisineringens påvirkningskraft. På den ene siden kan vi se på utviklingen i de to gruppene hver for seg, også kalt før- og ettersammenligninger. De 42 personene i fluvastatingruppen fikk i gjennomsnitt endret sitt kolesterolnivå med -0,56 mmol/liter (tabell 2). Et 95 prosent konfidensintervall er da gitt ved [-0.80, -0.32] mmol/liter. Med referanse til vår tidligere beskrivelse av konfidensintervall kan vi si at hvis vi hadde gitt fluvastatin til alle stillesittende og overvektige norske menn med høyt blodtrykk så ville deres gjennomsnittlige kolesterolreduksjon ganske sikkert (95 prosent) ligget et sted mellom 0,32 og 0,80 mmol/liter.

Basert på konfidensintervallet over er det fristende å konkludere at fluvastatin reduserer kolesterolnivået til stillesittende og overvektige menn, men igjen må vi være forsiktig med å hoppe for raskt til en konklusjon. Hva om årsaken til kolesterolreduksjonen er at mennene inviteres til å delta i undersøkelsen? Hva om de som er med i undersøkelsen samtidig får større oppmerksomhet rundt sin egen helse og begynner å spise sunnere eller trene mer? Hittil har vi bare sammenliknet gjennomsnitt før og etter behandling. Vi kan derfor ikke utelukke at den egentlige årsaken til at kolesterolet endrer seg er at mennene får større oppmerksomhet rundt sin egen helse.

Sammenlikning av gjennomsnittet

Hvis vi ønsker å avgjøre om reduksjonen i kolesterolnivå faktisk skyldes fluvastatin og ingenting annet kan vi sammenlikne med gruppen som får placebomedisin. Med unntak av medisin/placebomedisin er nemlig alt likt mellom disse to gruppene. Ser vi ulike resultater i de to gruppene, må dermed årsaken ligge i selve medisinen. For placebogruppen ser vi at gjennomsnittlig endring er 0,00 mmol/liter (tabell 2). Tilhørende 95 prosent konfidensintervall er [-0.22, 0.22] mmol/liter. Sammenlikner vi de to konfidensintervallene ser vi altså potensielt langt større kolesterolreduksjon i fluvastatingruppen enn i placebogruppen.

De to konfidensintervallene over styrker oss i troen på at fluvastatin virker bedre enn placebo. Det finnes egne tester i statistikken som er laget nettopp for å bekrefte dette. I gjennomsnitt er bedringen 0,56 mmol/liter større i fluvastatingruppen enn i placebogruppen, og for denne gjennomsnittsforskjellen strekkes 95 prosent konfidensintervall fra 0,24 til 0,88 mmol/liter. Dette konfidensintervallet tar høyde for tilfeldige feilkilder i både placebo og fluvastatingruppen. Vi kan derfor si at hvis hele den aktuelle populasjonen hadde fått fluvastatin så ville gjennomsnittlig totalkolesterol med 95 prosent sannsynlighet gått ned 0,24 til 0,88 mmol/liter mer enn hvis den samme populasjonen hadde fått palcebomedisin. Siden den eneste forskjellen på de to gruppene er medisin/placebomedisin kan vi konkludere med at fluvastatin reduserer kolesterolnivået til stillesittende og overvektige menn med høyt blodtrykk.

I praksis vil forskjeller i gjennomsnitt og konfidensintervall ofte oppgis i samme åndedrag som en p-verdi. Selv om konfidensintervall og p-verdier ofte gir overlappende informasjon er de resultater av litt ulike tilnærmingsmåter. P-verdier er et resultat av hypotesetester, og det er ikke fritt for at mange ser på denne p-verdien som noe magisk og absolutt. I neste nummer av Sykepleien Forskning skal vi ta en nærmere titt på hypotesetester, p-verdier og fortolkningen av disse.

Referanser

1) Brurberg KG, Hammer HL. Hvorfor trenger vi statistikk? Sykepleien Forskning. 2013;8(1): 78-82.

2) Bjørndal A, Hofoss D. Statistikk for helse- og sosialfagene. Gyldendal akademisk, Oslo. 2004

3) Hjelstuen A, Anderssen SA, Holme I, Seljeflot I, Klemsdal TO. Effect of lifestyle and/or statin treatment on soluble markers of atherosclerosis in hypertensives. Scandinavian Cardiovascular Journal. 2007;41:313-20