Hva var resultatene?

I artikkelen Å vurdere kunnskap tar vi opp hvordan det går an å finne ut om det som står i en forskningsartikkel, er sant (1). Vi viste fremgangsmåter som øker sannsynligheten for at det en forsker har funnet ut og presenterer, er et riktig bilde av virkeligheten.

For å vurdere dette viste vi til spørsmål fra noen sjekklister for kritisk vurdering av forskning. Et eksempel på et slikt spørsmål var om tilfeldig fordeling av personer til en intervensjons- eller kontrollgruppe i en effektstudie øker sjansen for at gruppene blir sammenliknbare.

Resultatene

Vi tok ikke opp spørsmålet om hva resultatene var. Det må vi også kunne bedømme før det gir mening å gå videre med artikkelen. Vi må vite hva resultatene betyr, før vi eventuelt tar funnene videre ved å bruke dem i faglige retningslinjer eller iverksette tiltak som endrer praksis. Vi må vite om resultatene av en primærstudie eller fra en systematisk oversikt virkelig tyder på at et tiltak gir helsegevinst, om det skader, eller om det ikke har effekt i det hele tatt.

Statistikk

Når vi skal oppsummere kvantitative resultater, er faget statistikk nyttig. Statistikken har noen verktøy som gjør det enklere å oppsummere resultatene. Å beregne et gjennomsnitt er et eksempel. Noen andre statistiske mål blir nevnt senere.

I tillegg hjelper statistikken oss til å ta høyde for graden av tilfeldig variasjon. Hvis du ser en effekt av et tiltak, kan den nemlig skyldes rene tilfeldigheter. En statistisk vurdering hjelper oss med å bedømme hvor stor feilmargin resultatet er beheftet med.

Statistikk kan man lære seg på ulike nivåer. Noe må man lære seg for å vurdere et kvantitativt arbeid, men det er ikke nødvendig å bli ekspert. I denne artikkelen farer vi nokså lett over statistikken, og du vil behøve mer utfyllende litteratur (2–5).

Å bedømme effekt

Effektspørsmål handler om tiltak som settes i gang innen forebygging, behandling eller rehabilitering. Eksempler på slike spørsmål er:

• For gutter i alderen 16 til 18 år, fører gratis tilgjengelig kondomer til at færre får klamydiainfeksjon?
• For pasienter over 70 år med leggsår, hva er effekten av ettlagsbandasje sammenliknet med firelagsbandasje på sårtilheling?
• For kvinner som har fått diagnosen brystkreft, vil trening i grupper med fysioterapeut gi bedre livskvalitet?

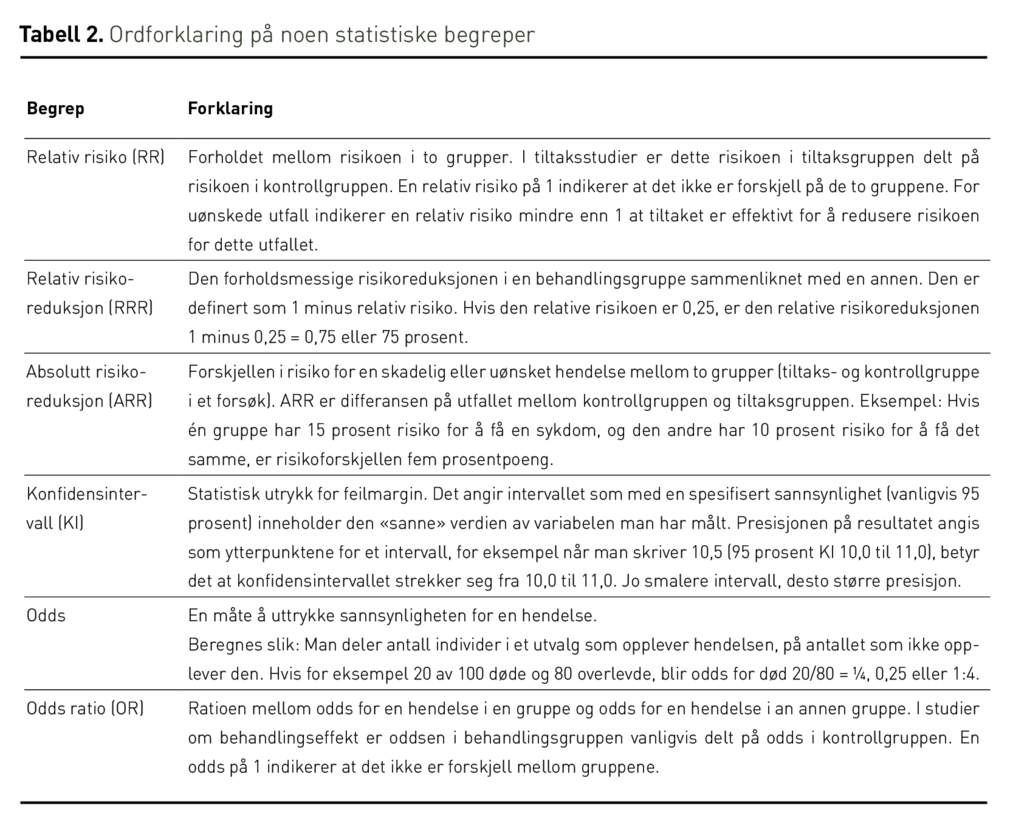
Som regel måler vi effekt av forebygging og behandling ved å telle negative hendelser, for eksempel sykdom eller død, blant dem som fikk, og dem som ikke fikk tiltaket. To vanlige måter å presentere forskjellen på er «absolutt risikoreduksjon» (ARR) og «relativ risikoreduksjon» (RRR).

Tenkt eksempel:

Hvis risikoen for et negativt utfall i behandlings-/intervensjonsgruppen var 4 prosent, og risikoen var 10 prosent i kontrollgruppen, er den absolutte risikoreduksjonen (ARR) 6 prosent (10 prosent – 4 prosent), eller mer korrekt: 6 prosent poeng.

Den relative risikoreduksjonen (RRR) blir i dette tilfellet 60 prosent, ettersom nedgangen på 6 prosentpoeng tilsvarer 60 prosent av utgangsrisikoen (10 prosent). Utregningen av RRR blir her 1 – [4/10] = 0,6 eller 60 prosent.

Talleksempel

Eksempelet nedenfor er hentet fra boken til Trish Greenhalgh (3). Spørsmålet er om hjertekirurgi øker sjansen for overlevelse blant hjertepasienter sammenliknet med bare å gi dem medisinsk behandling i form av tabletter og vanlig oppfølging.

En enkel utregning forteller deg at pasienter som fikk medisinsk behandling, hadde en 404 / 1325 = 0,305 eller 30,5 prosent sjanse for å være døde etter ti år. La oss kalle dette tallet for risiko X. Pasienter tilfeldig fordelt (randomisert) til kirurgisk behandling hadde en 350 / 1324 = 0,264 eller 26,4 prosent sjanse for å være døde etter ti år. La oss kalle dette tallet for risiko Y.

Den relative risikoen (RR) for død, det vil si risikoen for død blant de opererte sammenliknet med kontrollgruppen som fikk medisinsk behandling, er Y delt på X, det vil si 0,264 / 0,305 eller 0,87 (87 prosent).

Den relative risikoreduksjonen (RRR), som betyr hvor mye risikoen for død blir redusert ved kirurgi, er 100 prosent – 87 prosent (1 – Y/X) og blir 0,13 eller 13 prosent.

Den absolutte risikoreduksjonen er X minus Y (30,5 prosent – 26,4 prosent), det vil si 4,1 prosent (0,041).

Den siste måten å uttrykke effekt på som vi skal omtale, er utbredt, men ikke intuitivt helt enkel å forstå, nemlig odds ratio (OR). Odds er sjansen for det ene utfallet dividert med sjansen for det andre utfallet. Odds for å dø sammenliknet med odds for å overleve i den medisinske gruppen er 404 (døde) / 921 (levende) = 0,44. For pasienter i kirurgigruppen er det tilsvarende tallet 350 (døde) / 974 (levende) = 0,36. Forholdet, eller ratioen, mellom disse sjanseberegningene (odds ratio) er 0,36 / 0,44 = 0,82.

Om denne undersøkelsen – som sammenlikner kirurgisk og medisinsk behandling av en alvorlig lidelse – kan vi derfor konkludere følgende:

Kirurgi reduserer dødeligheten med 13 prosent.

Kirurgi gir en absolutt reduksjon i sjansen for å dø på 4 prosent.

Kirurgi øker sjansen for å overleve fra 70 til 74 prosent.

Alle måtene å uttrykke seg på er «korrekte», men de etterlater litt forskjellig inntrykk. Det krever litt trening å turnere disse forskjellige uttrykkene. Den viktigste treningen får du ved å lese artikler og forsøke å forstå hva resultatene er, og se hvordan de er tallfestet. Øvelse gjør mester!

Konfidensintervall

Hver gang vi forsøker å beregne en effektstørrelse i et forsøk, må vi reflektere over innslaget av tilfeldig variasjon. Et forsøk vil gi ett resultat. Hvis vi gjorde det samme forsøket om igjen på nye pasienter, ville vi finne en effekt i samme størrelsesorden, men vi ville ikke finne akkurat det samme tallet. Hvor mye tilfeldig variasjon vi må regne med, avhenger av 1) hvor mye informasjon som er tilgjengelig, det vil si hvor stort utvalg som er med i forsøket, og 2) hvor mye underliggende variasjon det er i det fenomenet vi prøver å påvirke.

En måte å kvantifisere den tilfeldige variasjonen som alltid følger med en måling på, er å beregne et konfidensintervall der vi kan være rimelig (for eksempel 95 prosent) sikre på å finne den sanne verdien. Hvis den absolutte risikoreduksjonen i et forsøk var 6 prosent og vi beregner et 95 prosent konfidensintervall som gikk fra 2 til 9 prosent, er det dette intervallet vi har tillit (konfidens) til.

Med andre ord: Hadde vi gjort forsøket om igjen, hadde gevinsten sikkert ikke vært en risikoreduksjon på akkurat 6 prosent, men med en 95 prosent sannsynlighet hadde vi funnet et tall mellom 2 og 9 prosent.

Et slikt konfidensintervall eller feilmargin viser oss med hvilken presisjon en effekt er bedømt. Du vil sikkert være enig i at en 20 prosent reduksjon i dødelighet som har et smalt konfidensintervall, for eksempel 18 til 23 prosent, er «mer til å stole på» enn en tilsvarende reduksjon med en stor feilmargin, for eksempel 6 til 45 prosent. Hvis konfidensintervallet inneholder tallet null og for eksempel går fra –5 til 60 prosent, kan vi ikke med rimelig grad av sikkerhet utelukke at behandlingen har null effekt (eller endog skader).

Se også statistikksidene på kunnskapsbasertpraksis.no (4).

Denne artikkelen er en revidert versjon av en artikkel som tidligere er publisert (6).

Referanser

1.     Reinar LM. Å vurdere forskning. Sykepleien Forskning. 2007;1(2):126–9.

2.     Bjørndal A, Hofoss D. Statistikk for helse- og sosialfagene. Revidert utgave. Oslo: Gyldendal; 2004.

3.     Greenhalgh T. How to read a paper – the basics of evidence-based medicine. 4. utg. Oxford: Wiley & Blackwell Publishing, BMJ-books; 2010.

4.        Kunnskapsbasertpraksis.no. [internett]. Oslo: Folkehelseinstituttet; [sitert 23.05.2018]. Tilgjengelig fra: http://www.helsebiblioteket.no/kunnskapsbasert-praksis

5.     Nortvedt MW, Jamtvedt G, Graverholt B, Nordheim LV, Reinar LM. Jobb kunnskapsbasert! En arbeidsbok. 2. utg. Oslo: Akribe; 2012.  

6.     Reinar LM, Bjørndal A. Hva var resultatene? Tidsskrift for jordmødre. 1999;(5):15–8.