Viktige modeller og begreper i statistikk

Når du skal lese forskningsartikler, kan det være nyttig at du kjenner navnet på noen viktige modeller og begreper.
Her vil vi se på enkelte begreper og modeller i statistikk som du fra tid til annen vil støte på når du leser forskningsartikler.
Korrelasjon
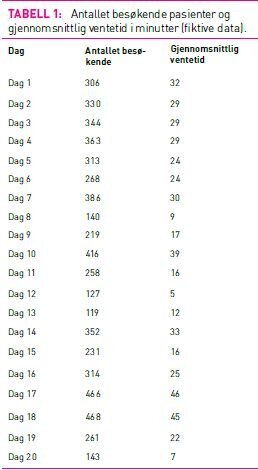
Utforskning av sammenhenger står svært sentralt i statistikken, og vi har tidligere sett på sammenhengen mellom statiner og kolesterolreduksjon (1). Tabell 1 viser antall besøkende på et akuttmottak sammen med gjennomsnittlig ventetid per pasient (fiktive data). Av tabellen ser vi sterke indikasjoner på en sammenheng mellom antall besøkende og ventetid. For dagene 10, 17 og 18 er det over 400 besøkende, og gjennomsnittlig ventetid er nærmere tre kvarter. På dag 8, 12 og 20 er det få besøk, og ventetiden er under ti minutter. Sammenhengen blir enda lettere å se når vi plotter data som vist i figur 1.
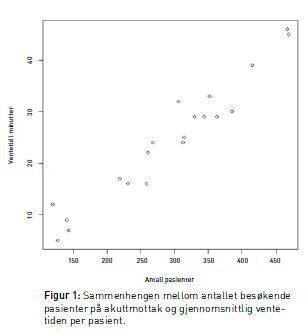
Det går an å regne på graden av samsvar mellom to variabler. Et mye brukt mål er lineær korrelasjon (Pearson korrelasjon), et korrelasjonsmål som alltid ligger mellom -1 og 1. Dess nærmere korrelasjonen er -1 eller 1, dess sterkere er sammenhengen mellom de to variablene. Fortegnet viser retningen på sammenhengen. For data i figur 1 er korrelasjonsmålet 0,967 som betyr at vi har en svært sterk sammenheng mellom antall besøk og ventetid. Vi sier at korrelasjonen er positiv fordi flere besøk gir økt ventetid. Et eksempel på negativ korrelasjon kan være sammenhengen mellom antallet timer en person trener kondisjon og tiden han/hun trenger for å løpe 3000 meter. Korrelasjonen er negativ idet økt treningsmengde fører til at tiden man bruker går ned. Figur 2 illustrerer hvordan data kan se ut for ulike korrelasjoner. Ventetidsdataene i figur 1 likner mest på dataene oppe til høyre i figur 2.

Korrelasjon er ikke kausalitet
Når vi observerer en sammenheng (signifikant korrelasjon) mellom to variable er det lett å tro at det finnes årsakssammenhenger, men dette kan føre til alvorlige feilslutninger. Flere studier har for eksempel vist at personer som røyker mye har en tendens til å skåre dårligere på intelligenstester enn personer som røyker lite eller ingenting (4). En person som røyker vil kanskje være fristet til å konkludere med at intelligensen vil øke i det øyeblikket røyken legges på hylla, mon det? Forklaringer for sammenhengen kan for eksempel være at personer med høyere intelligens er mindre fristet til å begynne å røyke, eller at sosioøkonomisk status henger sammen med både økt risiko for røykestart og redusert intelligensskår. Hvis en av disse to forklaringene er årsaken, hjelper det neppe mye på intelligensen å slutte å røyke. Korrelasjonsstudier forteller altså ikke hva som forårsaker funnene. Til det trengs andre typer observasjoner og analyser.
Lineær regresjon
Lineær regresjon støter du oftest på i studier der forskerne observerer en rekke individer over tid og senere utfører statistiske analyser. Vi kan for eksempel være interessert i å studere sammenhengen mellom røyking og lungefunksjon. Siden vi ikke kan lage en studie der deltakerne i en gruppe pålegges å røyke, må vi nøye oss med observasjonsdata av lungefunksjon målt i en gruppe mennesker bestående av både røykere og ikke-røykere. Da kan det være fristende å sammenlikne lungefunksjon i de to gruppene direkte, men som vi skal se kan en slik tilnærming gi svært gale resultater.
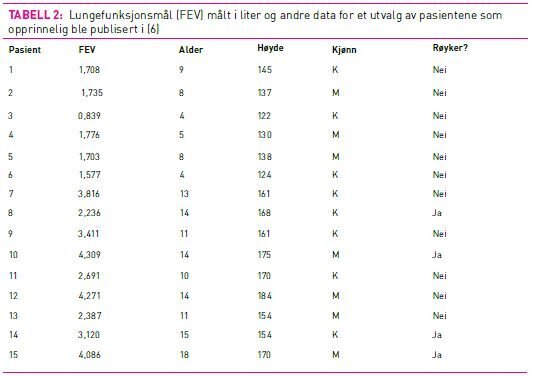
Tabell 2 viser et utvalg av data som opprinnelig ble analysert i (5). FEV er et lungefunksjonsmål som viser hvor mye luft en pasient evner å puste ut i løpet av et sekund. I tillegg til FEV har vi for hvert barn/ungdom informasjon om alder, høyde, kjønn og røykestatus. Totalt ble det gjennomført målinger for 654 barn og unge mellom 3 og 19 år. Hvis vi beregner korrelasjonen mellom FEV og røykestatus får vi 0,25 med 95 prosent konfidensintervall fra 0,17 til 0,32. Ifølge disse resultatene har barn/unge som røyker bedre lungefunksjon enn de som ikke røyker. Et slikt resultat er overraskende og skyldes at andre faktorer lurer i kulissene. Videre analyser viser nemlig at det er en korrelasjon både mellom alder og FEV og mellom alder og røyking. Det betyr – ikke overraskende – at lungefunksjonen bedres etter hvert som barna vokser, og at det i all hovedsak er de eldste i datasettet som røyker. Den egentlige (og negative) sammenhengen mellom røyking og lungefunksjon er totalt overskygget av den sterke positive sammenhengen mellom alder og FEV. Vi sier at alder er en konfunderende (confounding) variabel for sammenhengen mellom FEV og røyking.
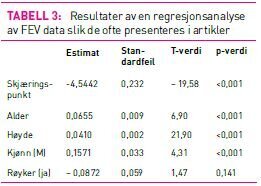
Ved bruk av lineær regresjon kan man i større grad isolere effekten av en og en faktor. Vi ønsker nå å bruke lineær regresjon til å undersøke hvilke faktorer som kan forutse (predikere) lungefunksjon (FEV). Vi sier at FEV er den avhengige variabelen i analysen. Faktorene vi bruker til å predikere FEV, her vil det si alder, høyde, kjønn og røykevaner, kalles uavhengige variabler. Tabell 3 viser resultatet av en regresjonsanalyse slik de gjerne presenteres i forskningsartikler. Lengst til høyre i tabellen ser vi en kolonne med p-verdier, og vi ser at alder, høyde og kjønn har svært små p-verdier. Det betyr at vi har en sterk sammenheng mellom FEV og disse faktorene. I kolonnen «Estimat» ser vi at verdiene er positive for alle tre variablene, som betyr at vi har en positiv sammenheng mellom FEV og disse variablene, for eksempel at FEV blir høyere med alder. Verdien 0,0655 sier oss at hvis vi sammenlikner to barn/unge med ett års aldersforskjell, men som har samme høyde, kjønn og røykevaner, vil FEV i gjennomsnitt være 0,0655 liter høyere hos den eldste. Vi har altså isolert effekten av alder. Tilsvarende ser vi at en gutt vil ha en FEV som i gjennomsnitt er 0,157 liter høyere enn ei jente så lenge de to har samme alder, høyde og røykevaner. En person som røyker vil derimot ha en FEV som i gjennomsnitt er 0,0872 liter lavere enn eller lik en ikke-røyker. Rett nok er ikke denne sammenhengen statistisk signifikant (p-verdi 0,141), men dette resultatet er mer i tråd med det vi vet om røykingens negative effekter enn da vi kun så på korrelasjonen mellom røyking og FEV. Vi kan si at regresjonsanalysen har hjulpet oss med å kontrollere for alder, høyde og kjønn.
Logistisk regresjon
Vi har sett hvordan vi kan bruke lineær regresjon å finne ut hvilke faktorer som predikerer lungefunksjon i form av FEV. FEV er det vi kaller et kontinuerlig mål (3). Logistisk regresjon er en nær slektning av lineær regresjon som brukes når den avhengige variabelen ikke er kontinuerlig, men består av kategorier som død versus levende. Ved hjelp av logistisk regresjon kan vi eksempelvis beregne hvordan faktorer som kjønn og alder (uavhengige variable) påvirker sannsynligheten for overlevelse (avhengig variabel). I likhet med lineær regresjon kan vi bruke logistisk regresjon til å isolere ulike effekter og kontrollere for forskjeller mellom grupper.
ANOVA
Vi har tidligere vist hvordan statistikk kan brukes til å sammenlikne to grupper, for eksempel for å påvise forskjeller mellom statiner og placebo (1). Det er lett å forestille seg naturlige utvidelser av et slikt eksperiment som involverer mer enn to grupper. Kanskje ønsker vi å sammenlikne effekten av ulike doseringer eller medisiner mot hverandre. Når vi har behov for å sammenlikne flere enn to grupper, er ANOVA (variansanalyse) et mye brukt verktøy. I variansanalyser er det, som navnet tilsier, den observerte variansen og ikke gjennomsnittsverdier som danner utgangspunkt for analysene.

Ved bruk av ANOVA kan vi altså studere effekten av flere faktorer samtidig. Tenk at vi ønsker å studere den kombinerte effekten av statiner og trening på reduksjon av kolesterol. For å undersøke dette kan vi lage oss et oppsett der forsøkspersonene plasseres tilfeldig i fire grupper (tabell 4). Vi ser at pasientene i gruppe 2 får statiner i tillegg til et spesifikt treningsprogram. Personene i gruppe 3 får placebomedisin og ikke noe treningsprogram. Ved bruk av ANOVA kan vi nå undersøke effekten av statiner og trening, og samtidig kan vi finne ut om kombinasjonen av statiner og trening har ytterligere effekt enn statiner eller trening alene. På tilsvarende måte som når vi sammenlikner to grupper (2), er signifikans, p-verdi og konfidensintervall viktige tall å se etter i artikler hvor ANOVA benyttes.
Ikke-parametriske tester
Vi har tidligere sett eksempler på sammenlikning av to grupper (2), og i denne artikkelen har vi beskrevet hvordan vi kan sammenlikne flere grupper (ANOVA). Disse testene baserer seg på antakelsen om at dataene i de ulike gruppene er tilnærmet normalfordelte. I mange situasjoner kan vi ikke gjøre denne antakelsen om dataene. Heldigvis finnes det tester for disse situasjonene også. Når du skal lese forskningsartikler, kan det være nyttig at du kjenner navnet på de mest vanlige testene. Skal to grupper sammenliknes er det vanlig å benytte Mann–Whitney U-test som også ofte refereres til som Wilcoxon rank-sum-test eller Wilcoxon-Mann-Whitney-test. Ved sammenlikning av mer enn to grupper benyttes vanligvis Kruskal-Wallis test. Også for disse testene presenteres resultatene i form av p-verdier, så det er nyttig å se etter disse verdiene i teksten.
Referanser
- Brurberg KG, Hammer HL. Hvordan sammenlikne statistisk? Sykepleien Forskning. 2013;8:174–7.
- Brurberg KG, Hammer HL. Hypotesetesting. Sykepleien Forskning. 2013;8:267–9.
- Brurberg KG, Hammer HL. Variabeltyper og dikotome effektmål. Sykepleien Forskning 2013; 8:372–4.
- Weiser M, Zarka S, Werbeloff N, Kravitz E, Lubin G. Cognitive test scores in male adolescent cigarette smokers compared to non-smokers: a population-based study. Addiction 2009;105:358–63.
- Tager, IB, Weiss, ST, Rosner, B, & Speizer, FE. Effect of parental cigarette smoking on pulmonary function in children. American Journal of Epidemiology. 1979;110:15–26.


















0 Kommentarer