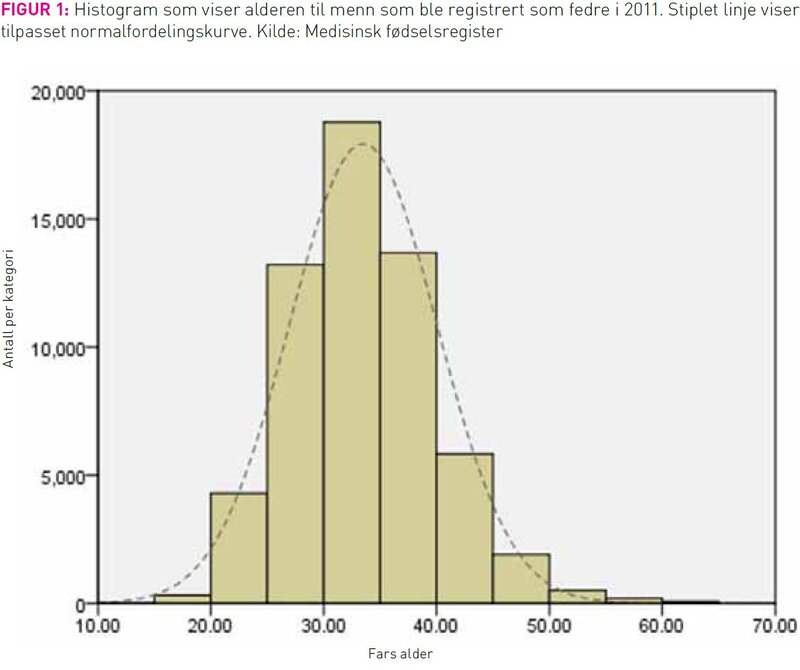
For mange formål er det upraktisk å samle statistikk om hele populasjonen. Et av hovedformålene med bruk av statistikk er nettopp å trekke slutninger om en populasjon basert på et mindre utvalg. Hvis du vil vite hvor mange av mennene som ble fedre i 2011 som var til stede under fødselen, er det upraktisk å spørre alle de 60000 som ble fedre dette året. Isteden kan vi spørre et utvalg av dem som ble fedre. Hvis vi spør 1000 nybakte fedre, og får vite at 95 prosent var til stede under fødsel, kan vi velge å generalisere til alle norske fedre (populasjonen) og anta at 95 prosent av alle fedre er til stede under fødsel i Norge.

Generalisering fra et utvalg til en større populasjon er ikke alltid rett frem. På den ene siden må vi være klar over at tilfeldigheter kan lure oss. Hvis vi hadde spurt ti fedre istedenfor 1000 kan det godt hende at alle hadde vært til stede på fødestua, men det er også ganske stor sjanse for at vi finner to personer som ikke var til stede under fødsel blant de ti spurte. En viss usikkerhet må vi lære å leve med, men statistikken hjelper deg med å synliggjøre hvor stor denne usikkerheten er. Hvis usikkerheten er større enn du er villig til å akseptere kan du iverksette tiltak i et forsøk på å redusere usikkerheten, for eksempel ved å øke utvalgsstørrelsen.

Synliggjør usikkerhet

Statistikken hjelper oss først og fremst med å synliggjøre grad av usikkerhet, og bidrar i mindre grad til å fjerne denne usikkerheten. Sitter du med dårlige data er det begrenset hva statistikken kan hjelp deg med, for statistikken er ikke en tryllestav som skaper gull av gråstein. Mange ser likevel på statistikk som en fortryllende svart boks der man lemper inn tall i den ene enden og får et ferdig fordøyd svar ut i den andre. En slik innfallsvinkel kan være farlig. Det å sette tall inn i en formel vil alltid gi et svar, men uten bakgrunnskunnskap er det vanskelig å vite hva svaret betyr og om det er til å stole på.

La oss gå tilbake til vår spørreundersøkelse blant nybakte fedre der vi spurte om hvor mange som var til stede under fødselen. Av 1000 spurt var 95 prosent til stede under fødsel, og vi konkluderte med at cirka 95 prosent av alle norske menn er til stede på fødestua når barn blir født. En forutsetning for en slik generalisering er at de som ble spurt (utvalget) gjenspeiler den norske befolkningen (populasjonen) på en god måte. Hvis data om fedres tilstedeværelse under fødsel baserer seg på undersøkelser ved ett bestemt sykehus kan vi gå glipp av variasjoner som forekommer på landsbasis, og da kan en generalisering gi et feilaktig totalinntrykk. Statistikken forutsetter at du ser på et representativt utvalg, men varsler deg ikke om betingelsen er oppfylt. Du trenger derfor kunnskap om både statistikk og forskningsmetode når du skal vurdere om du kan stole på resultatene av en studie.

Statistiske fordelinger

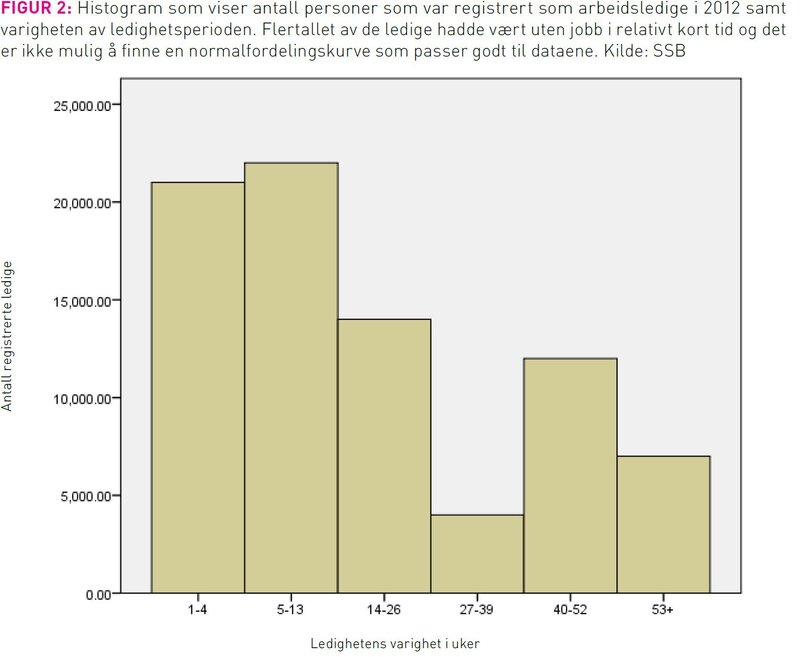
Alder er en kontinuerlig måleenhet, og histogrammet i figur 1 viser hvordan nybakte fedre fordeler seg i ulike alderskategorier. I eksempelet valgte vi å benytte 11 alderskategorier à 5 år (søylebredder), og vi ser at histogrammet antar en tilnærmet klokkeform (stiplet linje). Formen ville kommet enda tydeligere frem hvis vi hadde laget histogram med mer finmasket aldersinndeling (smalere søyler). I statistikken ser vi ofte histogram med en slik klokkeform, og vi sier da at data følger en Gauss- eller normalfordelingskurve. Normalfordelingskurven er symmetrisk, det vil si at kurven er like bratt enten man beveger seg fra midten mot venstre eller fra midten mot høyre. I tillegg til at slike symmetriske data ofte dukker opp i reelle situasjoner, har normalfordelingen en del egenskaper som gjør matematikere glade. Det er derfor ikke uten grunn at normalfordelingen er blitt statistikkens viktigste sannsynlighetsfordeling. I den virkelige verden finnes det mange eksempler på data som nekter å innordne seg etter normalfordelingens klokkeform. Figur 2 oppsummerer norske arbeidsledighetstall fra 2012 og illustrerer skjevfordelte data som ikke passer med normalfordelingen. Siden normalfordelingen ikke alltid passer med virkeligheten har statistikere utviklet andre fordelingskurver for diverse formål, blant annet Kjikvadratfordelingen, Fisherfordelingen, Rektangulærfordelingen, Poissonfordelingen og Den binomiske fordelingen. I denne omgang begrenser vi ambisjonsnivået til å nevne at disse finnes.

 

 

 

Referanser

1. Sutherland S. Irrationality. Pinter & Martin, London. 1992.

2. Goldacre B. Bad science. Fourth Estate, London. 2008.

3. Wootton D. Bad medicine. Doctors doing harm since Hippocrates. Oxford University Press, Oxford. 2006

4. Nortvedt MW, Jamtvedt G, Graverholt B, Nordheim LV, Reinar LM. Jobb kunnskapsbasert! Akribe, Oslo. 2012.